Excelで始めるSFCモデル入門 - 好奇心の横断歩道を創る！

導入
シート「表と恒等式一覧」
シート「行動方程式と定義式」
シート「モデルの式一覧」
シート「実行とプロット」
最後に

導入

非常にシンプルなSFCモデルを、Excelで実装したものを説明する。PCで読まれることを想定している。

SFCモデルとは何か？についてはこちらで書く
github.com

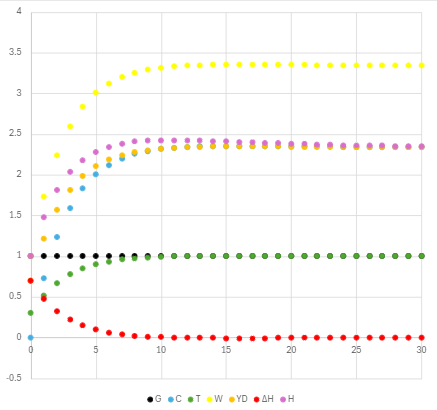
実装したものがこれ。

右下の4つのアイコンのうち、一番右をクリックすると、新しいタブに全画面表示される

「表と恒等式一覧」「行動方程式と定義式」「モデルの式一覧」「実行とプロット」の４つのシートがある。順番に説明する

シート「表と恒等式一覧」

「表と恒等式一覧」では、ストック・フロー一貫モデルがその定義上満たさなければならない恒等式が示されている

取引フロー表

	家計	企業	政府	合計
消費	$-C$	$+C$		$0$
政府支出		$+G$	$-G$	$0$
賃金	$+W$	$-W$		$0$
税	$-T$		$+T$	$0$
貨幣の変化	$-\Delta H$		$+\Delta H$	$0$
合計	$0$	$0$	$0$

取引フロー表は、フローの会計的整合性を表す恒等式群を、視覚的に表している。今回の取引フロー表では、以下の恒等式が成立している必要がある
$-C+W-T-\Delta H=0$
$+C+G-W=0$
$-G+T+\Delta H=0$
この３つの恒等式のうち任意の１つは、それ以外の２つから導出される。
２つの恒等式を使えばおのずとモデルのフローの会計的整合性は担保されるので、今回のモデルでは、 $+C+G-W=0$ と $-G+T+ΔH=0$ を使う。
モデルが完成した後で、 $-C+W-T-ΔH=0$ が成立しているかどうかを確認することで、モデルの会計的整合性を確認する。このような恒等式は隠れた等式（Hidden equation）などと呼ばれる。

ストックとフローの整合性を表す恒等式として、以下の恒等式も満たされる必要がある。
$H=H_{-1}+\Delta H$
下付き文字-1は、その変数の前期の値を示す。期末の貨幣残高が、期首の貨幣残高と貨幣残高の変化の和であらわされる。

シート「行動方程式と定義式」

変数を定義するための式を定義式と呼び、今回は可処分所得 $YD$ を
$YD=W-T$
と定義する。

行動方程式は、各部門がどのような意思決定で支出などの金額を決定するかを示す。モデルが採用する仮定が反映される。今回のモデルでは以下の行動方程式が採用される。
$G=1$
$C=\alpha_1 YD_{-1}+\alpha_2 H_{-1}$
$T=θ(C+G)$
$W=C+G$
ギリシャ文字はパラメータ。

シート「モデルの式一覧」

モデルの式を一覧する。式の右辺の変数は、左辺の変数よりも先に計算されている必要がある。今回はこの順番で計算することで、右辺の変数が左辺の変数よりも先に計算される。
$G=1$
$C=\alpha_1 YD_{-1}+\alpha_2 H_{-1}$
$T=\theta (C+G)$
$W=C+G$ (恒等式 $+C+G-W=0$ を $W$ について解いたもの)
$YD=W-T$
$\Delta H=G-T$ (恒等式 $-G+T+\Delta H=0$ を $\Delta H$ について解いたもの)
$H=H_{-1}+ΔH$
この７つの式が、今回のモデルである。

モデルの内生変数 $C,T,W,YD,\Delta H,H$ の値を決定するためには、パラメータの値と一部の内生変数の初期値(今回のモデルでは $YD, H$ )の値を定めなくてはならない。そこで、パラメータの値と、全ての内生変数の値を定めておく

パラメータ	値
$\alpha_1$	$0.9$
$\alpha_2$	$0.1$
$\theta$	$0.3$

内生変数の初期値	値	初期値同士の関係
$C_{(t=0)}$	$0$
$T_{(t=0)}$	$\theta$	$T_{(t=0)}=\theta \{C_{(t=0)}+G_{(t=0)}\}$
$W_{(t=0)}$	$1$	$W_{(t=0)}=C_{(t=0)}+G_{(t=0)}$
$YD_{(t=0)}$	$1-\theta$	$YD_{(t=0)}=W_{(t=0)}-T_{(t=0)}$
$\Delta H_{(t=0)}$	$1-\theta$	$\Delta H_{(t=0)}=G_{(t=0)}-T_{(t=0)}$
$H_{(t=0)}$	$1$