好奇心の横断歩道を創る！

自分の思考をラバーダック・デバッグするためのブログ

トップ > SFCモデル > 政府支出を税収の一定倍とする、解析的に解けるSFCモデル

政府支出を税収の一定倍とする、解析的に解けるSFCモデル

SFCモデル

動機

前にこんなの
rokabonatttsu.hatenablog.com
を書いたんだけど、政府の支出は外生的と言うよりも財政収支0を目指す、と言われると、そんな気もしなくはない*1ので、政府支出を税収の一定倍にするものとして書き直してみた。解析的に解くために、非常にシンプルなモデルを用いる。
今回も閉鎖経済のモデル。開放経済のモデルは色々大変で、少なくとも解析的に解きたくない。

取引フロー表

家計 企業 政府 合計
消費 -C +C 0
政府支出 +G -G 0
賃金 +W -W 0
税 -T +T 0
貨幣の変化 -\frac{dH}{dt} +\frac{dH}{dt} 0
合計 0 0 0

式一覧

G=(1+\alpha)T
C=\beta_1YD+\beta_2H
W=C+G
T=\gamma W
YD=W-T
\frac{dH}{dt}=G-T

モデルでは使わないが、
\frac{dH}{dt}=-C+W-T

初期値設定とパラメータの値の範囲

初期値を定めないといけないのだが、今回はHの初期値を H_0として決める。他の変数の初期値もこれで定まる。
H_{(t=0)}=H_0

パラメータの値として想定している範囲は、
-1<\alpha<1
0<\beta_1, \beta_2, \gamma<1

解いた結果

H=H_0\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}t\}
G=\frac{(1+\alpha)\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}H_0\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}t\}
C=\frac{\beta_2(\alpha\gamma+\gamma-1)}{\alpha\gamma-\beta_1\gamma+\beta_1+\gamma-1}H_0\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}t\}
YD=\{\frac{\beta_2}{1-\beta_1}+\frac{\alpha}{1-\beta_1}\frac{\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}\}H_0\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}t\}
W=\{\frac{\beta_2}{1-\beta_1}+\frac{1+\alpha-\beta_1}{1-\beta_1}\frac{\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}\}H_0\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}t\}
T=\frac{\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}H_0\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}t\}
解く過程は
https://holistic-theater-fae.notion.site/SFC-17751e0c814280c2ae83e8e84d08274b
にある

パラメータの値を試しに定める

(\alpha, \beta_1, \beta_2, \gamma, H_0)=(0.05, 0.95, 0.02, 0.4, 1)
としてみると、
H=\exp(0.04t)
G=0.84\exp(0.04t)
C=1.16\exp(0.04t)
YD=1.2\exp(0.04t)
W=2\exp(0.04t)
T=0.8\exp(0.04t)
となる。グラフにするとこんな感じ。

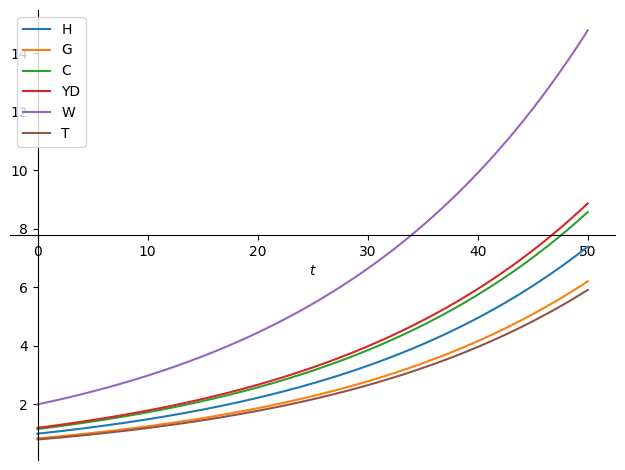
パラメータの値を変えると、モデルの質が大きく変わる。特に、貨幣でもあり政府債務残高でもある Hが、他の変数との比率を大きく変えやすい。きちんと調べていないからわからないが、体感では、外生的に政府支出を決めていたモデルよりもパラメータの変化に対して敏感に反応している、気がする。

最後に

「名目GDP成長率が高く維持されていると、労働者層も富裕層も消費に積極的になる(\beta_1, \beta_2が大きくなる)傾向があるんじゃないか？\beta_1, \beta_2が大きくなるとますます名目GDP成長率\exp\{\frac{\alpha\beta_2\gamma}{(1-\beta_1)-(1+\alpha-\beta_1)\gamma}\}-1が上がる。フィードバックループがあるならパラメータの値を外生的に定めるのは不適切では？」とか、パラメータの値を外生的に与えることの妥当性を疑う気持ちはありつつ、そんな難しいこと言われても自分にはどうすることも出来ないと諦めてこの記事を終わる。そもそもが過度に単純化したモデルなのだ。今更気にすることではない。

資本・投資と利潤を追加したモデルも作ろうとしたんだけど、計算の途中で異様に複雑化してしまって、面倒になってやめた。万が一気が向いたら、頑張って計算してここに結果を追記する。

*1:日本やアメリカでは法律的に財政均衡を目指していることになっているっぽいけど、有名無実化している感じはする。一方のユーロ圏なんかは政府の債務不履行リスクがあるから、財政収支を結構本気で気にしていそう。今回のモデルはユーロ圏の国にフィットするかな？と思ったけど、ユーロ圏であっても閉鎖経済のモデルを当てはめるのが明らかにまずい国はあって、例えば最近のドイツは経常収支対GDP比が5%超えを連発していたり、ギリシャは2023年まで4年連続-5%を下回っていたり、閉鎖経済のモデルとは程遠い。自国通貨の需給バランスが為替レートで調整されやすい国とは違い、そもそも経常収支対GDP比が0から乖離しやすいのかも。知らんけど。