自作のSFCモデルから、現実のデータと同じ性質が成立する様子を再現したい

名目GDPがほとんど変わらない中で政府債務残高対GDP比率が上昇する様子の再現
債務残高対GDP比率と、GDP成長率（単年ではなく中長期）の、負の相関関係

この記事で行うのは証明ではない。用いたモデルはあくまでモデルであって、現実ではないからだ。それから、外生的に与える歳出（名目）と内生的に与えられるGDP（名目）や税収（名目）や消費（名目）や投資（名目）が概ね比例する、みたいな現象は、ストック・フロー一貫モデルを作っているとあまりにもよく見られるので、ここでは触れない。何かあれば追加していくかもしれない

名目GDPがほとんど変わらない中で政府債務残高対GDP比率が上昇する様子の再現

「将来不安が高まるほど消費性向が下がり、可処分所得から消費に回す割合が下がり、税収が減り、分母の縮小と分子の拡大の両面から、政府債務残高対GDP比が大きくなる」「所得格差が大きくなるほど、消費性向が下がり、税収が減り、政府債務残高対GDP比が大きくなる」などという効果が現実にはあるはずだと個人的には思っているが、今回のモデルはその効果までは含まない。それでも、昔は政府の支出を積極的に増やしていたが最近はほとんど一定、という日本のような状況下で、政府債務残高対GDP比率が時間とともに上昇していく様子を再現する

使ったSFCモデルはこれ
github.com
モデルの詳細を知りたい方はこちらへどうぞ。

パラメータ $\beta$ は、物価不変の場合に政府の支出（公務員給与を含む）を前期比で概ね $1+\beta$ 倍に増やす、という意味を持つ。横軸 $t=0$ のタイミングで、 $\beta=0.02$ から $\beta=0$ に値を変え、バブル発生以前から2024現在までの様子をイメージした。 $\beta=0.02$ は、供給能力の成長率を少し上回るような政府支出増加率を目標にする水準。

見てわかるとおり、政府の支出が増加しなくなったタイミングt=0から政府債務残高対GDP比率が上昇していく。自然言語的な解釈をすれば、物価がコンスタントに上昇している間は、フローの名目値が上昇する分、政府債務残高が実質目減りする圧力がかかっている一方、政府の支出をほぼ一定にすると物価がほとんど不変あるいは低下し始め、政府債務残高の実質目減り圧力がなくなるから。かな。日本では、第二次世界大戦後しばらくインフレ率と財政支出成長率が高めの時期を経験し、バブル崩壊以後はインフレ率と政支出成長率が低めで推移している時期を経験しているので、最近の日本で政府債務残高対GDP比率が上昇していく様子を再現していると思う。

債務残高対GDP比率と、GDP成長率（単年ではなく中長期）の、負の相関関係

共通通貨や外貨を国内で流通させず（少なくとも租税単位に用いず）、固定為替制度を採用しない国については、「債務残高対GDP比率が高いからGDP成長率が下がる」という主張は、良くてほとんど関係ない、悪ければ完全な嘘だ、と思っている。では、先進諸国の債務残高対GDP比率とGDP成長率の間に負の相関がある現実を、どう説明するのか。下にその私なりの説明を書く。

上で使ったモデルは、推移をみる分には振動していても言いたいことは何とか伝わるが、これから作りたいのは散布図であり、その振動が決定的に影響を与えかねない。ということで前に作った解析的に解けるかなりシンプルなSFCモデルを用いる。
rokabonatttsu.hatenablog.com

このモデルにおいて、tが十分大きいとき、

政府債務残高対GDP比率 $\frac{H}{Y}$ は、 $\frac{1-\alpha_1-\theta}{\gamma-\alpha_1\gamma+\alpha_2-\alpha_1\alpha_2}$ に収束していく
期間 $\Delta t$ におけるGDP成長率( $\frac{Y_{(t)}-Y_{(t-\Delta t)}}{Y_{(t-\Delta t)}}$ )は、 $\exp(\gamma \Delta t) - 1$ に収束していく

$\gamma$ を除くパラメータは $0<\alpha_1, \alpha_2, \theta<1$ の条件を満たす。ここで仮に $\Delta t = 5, \alpha_1=0.68, \alpha_2=0.1, \theta=0.25$ として、唯一GDP成長率が収束する値に影響を与えるパラメータ $\gamma$ を動かしながら、縦軸＝債務残高対GDP比率が収束する値、横軸＝GDP成長率が収束する値で、散布図をプロットしてみると、

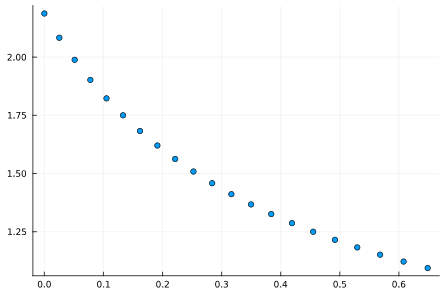
つまり、それぞれの国ごとに異なる財政支出成長率 $\exp(\gamma)-1$ で政府支出を拡大しているとき、政府債務残高対GDP比率とGDP成長率には負の相関が現れるということだ。このモデルにおける変数間の因果関係の向きは、外生変数として定義した財政支出が原因、内生変数として定義した消費・投資・貨幣残高・賃金・税が結果である。もちろんこのモデルは物価水準を定義しないし、そのほかほとんど最大限といえるレベルで簡略な記述を行ったモデルなので、「モデルが採用したのと同じ機序で現実でも負の相関が現れた、とは主張できない」との批判もできるが、私の直感はこのモデルの結果を現実の解釈に使っている

ちなみに、モデル上の政府債務残高対GDP比率が $A \equiv \frac{1-\alpha_1-\theta}{\gamma-\alpha_1\gamma+\alpha_2-\alpha_1\alpha_2}=\frac{1-\alpha_1-\theta}{(\gamma+\alpha_2)(1-\alpha_1)}$ に収束していくということは、現実によくあるパターンと同じく $\gamma \geq 0$ かつ $A>0$ ならば、 $1-\alpha_1-\theta>0$ が要求される。上の散布図のプロットに使った例も、それを満たしている。このとき、政府債務残高対GDP比率が収束する値は、パラメータの変化に対して

$\frac{\partial A}{\partial \gamma}=\frac{(1-\alpha_1-\theta)(-1+\alpha_1)}{(\gamma+\alpha_2)^2(1-\alpha_1)^2}<0$
$\frac{\partial A}{\partial \alpha_1}=\frac{(\alpha_2+\gamma)\{(1-\alpha_1)^2-\theta\}}{(\gamma+\alpha_2)^2(1-\alpha_1)^2}$
$\frac{\partial A}{\partial \alpha_2}=-\frac{(1-\alpha_1)(1-\alpha_1-\theta)}{(\gamma+\alpha_2)^2(1-\alpha_1)^2}<0$
$\frac{\partial A}{\partial \theta}=-\frac{1}{(\gamma+\alpha_2)^2(1-\alpha_1)^2}<0$

となる。つまり、このモデルでは、

政府支出の増加率を大きくするほど( $\gamma$ が大きくなるほど)、政府債務残高対GDP比率が収束する値が下がる
$\alpha_1$ の増加そのものは政府債務残高対GDP比率が収束する値を上げるかもしれないし、下げるかもしれない。 $\alpha_1<1-\sqrt{\theta}$ の範囲では、 $\alpha_1$ が大きくなるほど政府債務残高対GDP比率が上がる。 $1-\sqrt{\theta}<\alpha_1<1-\theta$ の範囲では、 $\alpha_1$ が大きくなるほど政府債務残高対GDP比率が下がる（ $1-\theta < \alpha_1$ は政府債務残高がマイナスになるので、現実的ではない）。 $\alpha_1$ の増加は、家計の金融資産が０の時の消費性向が増加する、みたいな意味。
$\alpha_2$ の増加は、政府債務残高対GDP比率が収束する値を下げる。 $\alpha_2$ の増加は、家計が金融資産保有に消極的になる、みたいな意味。
税率が上がるほど( $\theta$ の増加)、政府債務残高対GDP比率が収束する値を下げる