エージェントの位置座標をxとおく。x≧0の条件を付ける。エージェントの移動規則を、
(r:0から1までの一様乱数からのサンプル
dは分布の幅を左右するパラメータで、0<d<1。分布の幅のおおよその半値幅(1/2ではなく1/e)をHにしたいとき、d≒H ln {H sinh(1/H) } の近似が使える。)
こうすれば、エージェントの位置座標がx≥0において指数関数的に減衰する分布を示す。この分布の確率密度関数は、dの値にを使うことで、
に近づけることができる。エージェント数10^4、エージェント初期位置x=1、①と②を10^4回繰り返してみたところ、分布を示すヒストグラムがこんな感じになった。
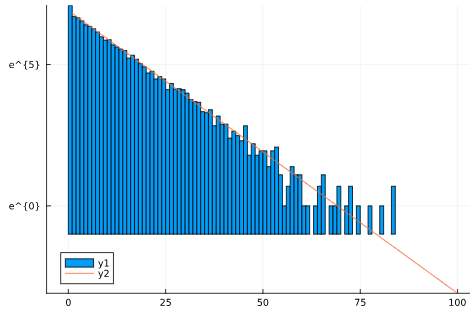
オレンジの線が目標にした確率密度関数の定数倍
対数スケールでほぼ直線的に減衰している様子から見て、指数関数っぽい分布になることは確かめられると思う。シミュレーションに用いたdは、にH=10を代入した時の値を用いた。xが10増えたときに1/eになる確率密度関数の定数倍が、オレンジの線。おおむね一致していることが確認できる。言い換えれば、うえで書いた移動規則を満たすとき、位置の確率密度が、狙った確率密度関数におおむね従うことがわかる。ただ、x=0のエージェントがやたらと多い。
証明、にはならないけれど、なぜこんなことを思いついたのかの説明を下に残しておく。いろんな意味でテキトーな説明しかできなかった。数学得意な人がひたすら羨ましい。
まず、エージェントの位置を表す確率変数Xと、エージェントの移動にかかわる確率変数Nを導入する。
Xの初期値X(t=0)の確率密度関数は、x≧0において 、x<0において
とする。エージェントの初期値が全員x=0にしたければ、λ_0=∞と思えば良い。
Nの確率密度関数g(x)は、-1-d ≦ x < 1-d においてg(x) = 1/2、それ以外の領域においてg(x)=0とする。
まず、XとNの和Yを考える。Xの確率密度関数は、x≧0においてλ exp(-λx) 、x<0においてf(x) = 0 で近似できる状態を維持すると仮定する。①と対応する部分。Yの計算は確率変数同士の和をとるときに、確率密度関数同士の畳み込み積分を行う。(以下の記事などを参照)
X(t)の確率密度関数がx≧0において 、x<0においてf(x) = 0 出かかれる場合のYを計算していく。
XとNがxの範囲によって異なる式で書かれる確率密度関数を持つので、Yの計算については積分範囲に気を遣う面倒さが伴うが、まぁ、そこは気合だけが頼り。ここには結果だけを記載しておく。
Yの確率密度関数は、私の計算が間違っていなければ、
0 (x<-1-d)
(1 - exp{-λ(x-1-d)})/2 (-1-d≦x<1-d)
(exp(-dλ) * sinh(λ) * exp(-λx) (1-d≦x)
となる。
続いて、Yのx<0の部分の積分値をAとおき、x<0の部分をx=0に圧縮する。②に対応する部分。圧縮後の確率密度関数で書かれる確率変数をX(t+1)とする。X(t+1)の確率密度関数は、ディラックのデルタ関数δ(x)を使って、
0 (x<0)
Aδ(0) (x=0)
(1-exp{-λ(x-1-d)})/2 (0<x<1-d)
exp{-dλ} * sinh(λ) * exp(-λx) (1-d≦x)
と書ける。X(t+1)が有限の値を持つ領域(x>0)のなかでも、そのほとんどの領域の確率密度が、exp{-dλ} * sinh(λ) * exp(-λx) で書かれている。X(t)の確率密度がx>0においてλ exp(-λx)で書かれていたので、exp{-dλ} * sinh(λ) ≒ λ であれば、t→t+1のときに確率変数Xの確率密度関数が同じような形になる。exp{-dλ} * sinh(λ) = λをdについて解くと、d=-(1/λ) * ln{λ/sinh(λ)} である。
①と②を繰り返したとき(t→∞)、Xの確率密度関数f(x)がx≧0においてf(x) = (1/H) exp(-x/H) になればうれしい。Xの確率密度関数f(x)がx≧0においてf(x) = λ exp(-λx) に近い形を維持しつつ、λ→1/H で安定すればうれしい。安定することを証明・説明することは私にはできないが、必要条件の一つにdの値を適切な値に設定することがあげられる。λ→1/H で安定するためには、dがd=-(1/λ) * ln{λ/sinh(λ)} にλ=1/Hを代入した値、つまりd=H * ln{H sinh(1/H)} に近い値をとる必要がある。