因子分析をはじめとする線形一次のモデルに現実味を感じなかったので、MCMCを勉強してみた。だって、現実の出来事は複数の要素の掛け算だったりエクスポネンシャルだったり、とにかくいろいろな種類の関係があるはずでしょう?
こちらのYoutube動画で、MCMCの中身を数学的になんとなく理解したつもりになってから、PyMC3でシンプルなモデルを作ってMCMCしてみた。モデルの適応範囲や、どの程度のことを主張できるか知っていたとしても、使えなきゃ面白くない。
まあ、白状すると、自分で書いたコードとはいえ、コメントアウトの内容が不適切かもしれないので、間違ったこと言ってるんじゃないかと疑いつつ読んでほしかったりする。
以下、実際に書いたコードと結果。
まずは必要な道具をインポートしておいて、

サンプルデータを自前で生成。

んで、サンプルデータを作った時と同じモデルを作って、MCMC

実行結果、こんな感じ。
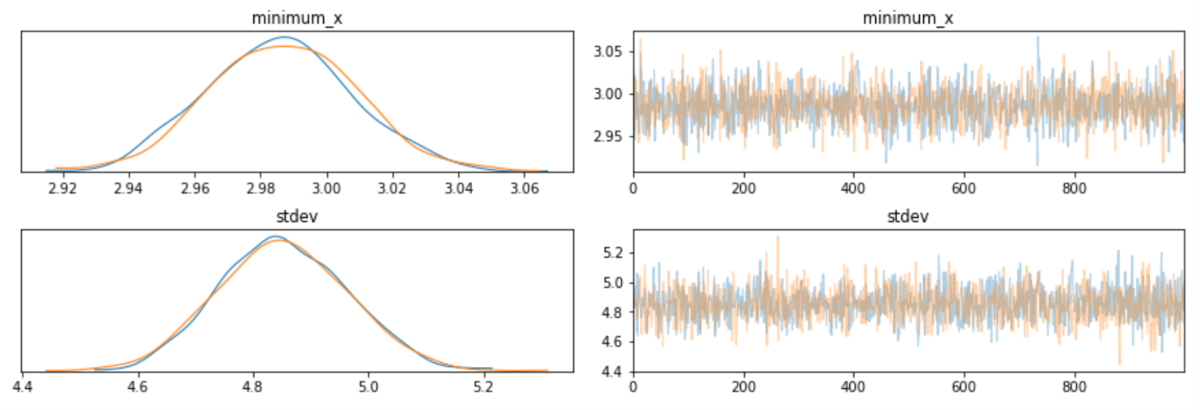
オレンジと青の2本の線があるのは、まあ、あまり気にしなくていいと思う。MCMCはそもそも確率的にパラメータを動かしてるので、2回同じことをやって、試行毎にどのくらい差が出るかの参考にしてるんじゃないかな。y=(x - 2.99)**2 あたりが適当なんじゃないかな?って結果。
続いて、無理やり線形のモデルでMCMCしてみた様子がこちら。

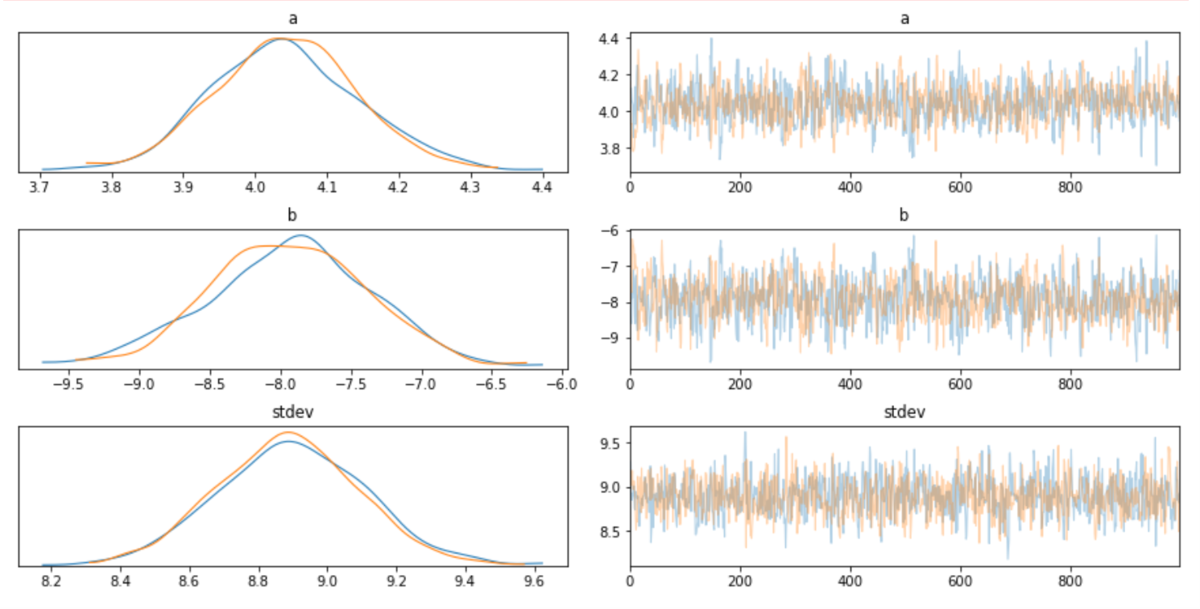
y=4.05*x - 8.0 あたりが適当なんじゃないかな?って結果。
さて、サンプルデータの生成と同じ関数(二次関数)のモデルでMCMCした場合と、サンプルデータ生成の方法とは全く合わない一次関数のモデルでMCMCした場合、それぞれのパラメータの尤度が出そろった。各パラメータで、最も尤度が高いと思われる数字を適当に選んで、サンプルデータと一つ目のモデルと二つ目のモデルを、同じグラフにプロットしたら、こんな感じ。
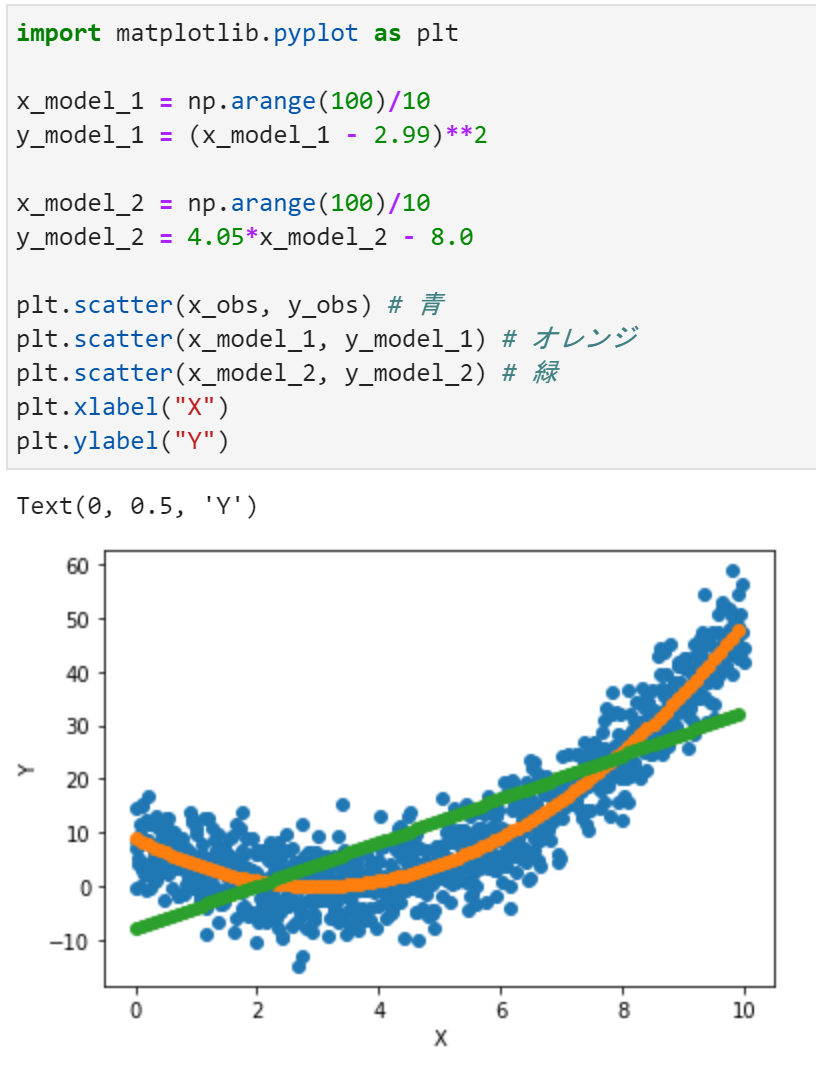
青がサンプルデータの散布図、
オレンジが1つ目のモデルでMCMCして、パラメータに適当な値を選んだもの、
緑が2つ目のモデルでMCMCして、パラメータに適当な値を選んだもの、
2つのモデルの優劣は一目瞭然ではないかな?因子分析みたく、線形一次でモデリングするのが嫌にならないかな?
話は以上。またいつか。